Benefits of Shear Keyed Surfaces in Precast Building

We have recently witne-ssed the coincidence between the Swiss SIA (SIA261) and the Indian Bureau of Standards (Is 1893, 6th revision) authorities, regarding the need of mechanisms to store quantities of energy during the seismic episodes and to enhance the collapsing in a ductile manner.

At the interface between two precast concrete surfaces working in shear, there are three factors contributing to the shear resistance:

• The cohesion of the concrete
• The forces normal to the interface surfaces
• The dowel action by steel bars protruding one of the concretes and inserted in the other one.

Depending on the finish of the concrete surface, different coefficients are assigned by the international codes in the calculation of the shear resistance.

The AMERICAN CONCRETE INSTITUTE Code ACI318, Nov.19, states the following:
From the table 16.4.4.2 – Nominal horizontal shear strength, of the same code, we can estimate that the concrete placed against hardened concrete intentionally roughened to a full amplitude of approximately 1/4 inch, mobilizes about 4 times more shear than the concrete placed against hardened concrete not intentionally roughened.

In Europe, the EUROCODE 2, in turn defines the geometries of the hardened concrete surfaces as very smooth, smooth (slipformed or extruded), rough and indented.

The European approach is as follows:

The shear design value VED must be less or equal to the shear resistance. The shear resistance vRdi must be less or equal to the friction mobilized by the shear key after cracking.

Both are summarized on the following equations :

Where:
C, µ are coefficients assigned by depen-ding on the surface finishing:
σn : force normal to the interface surface.
fctd: design tensile strength
fcd: design compressive strength (for αcc = 1)
The third term of vRdi in equation (1) is not considered because there is no armature protruding from the slabs and inserted on the grout pored at the longitudinal joint.
But the same European code EC2 in point 10.9.3 (12) reads that in diaphragm action of hollow core slabs with grouted joints, the average longitudinal shear VRDI must be limited to 0,15 MPa for smooth or rough surfaces.
In other words, based on the European code EN1992-1-1 (Eurocode 2), if they are smooth on their sides, all the extruded or the slipformed hollow core slabs existing or with installation in progress in the world on the date this article is published, have a longitudinal shear limited to vRdi =0,15 N/mm2 when they are meant to work in diaphragm action, which is the great majority of the cases.

Then the question is:
‘Would the pre-stressed concrete hollow core slabs be indented, what is the order of magnitude of the shear brough by this indenting on the hollow core slabs used in floors/roofs?’
We are interested in the value by itself and comparing it to this of the extruded and the slipformed hollow core slabs.

Numerical example:
STEP A: shear resistance generated by the indenting covering 50% of the effective height, 200 mm., on the 250 mm. hollow core slab side, when there is a force of 0,25 N/mm2 normal to the joint.
The 50% of the side surface smooth, generates:
vRdi = 0,2 * fctd + 0,6 * 0,25 N/mm2 = 0,2 * 1,2 + 0,6 * 0,25 = 0,39 N/mm2
The 50% of the side indented surface, generates:
vRdi = 0,5 * 1,2 + 0,9 * 0,25 = 0,825 N/mm2
Total vRdi = 1,21 N/mm2
On a length of 1,0 meter: V= 0,825* (1000*200/2) + 0,39 * (1000*200/2) = 121,5 kN/m If smooth, extruded or slipformed, the code limits to 0,15 N/mm2, therefore: V = 0,15 *(1000*200) = 30,0 kN/m
The additional shear force brought by the indenting is: 121,5 – 30,0 = 91,5 kN/m.

STEP B: friction generated by the 40 mm. concrete compression layer on the top of the slabs:
Vc = bw * d * fv = 1.200 mm * 0,04 * 0,63 = 30,24 kN/m (value 0,63N/mm2 following Walraven: ‘Shear under which no shear reinforcement is necessary in elements unreinforced in shear, general limit, for concrete C40 and thicknesses up to 200 mm.)
Therefore, we verify that the additional shear resistance of 91,5 kN/m is bigger to that of the compression layer 30,24 kN/m.

STEP C: If we fit #10 teeth as per the figure below and height 100 mm in a slab length of 1,0 meter, according to the example shown, the resistance of each indenting submitted to compression will be the following:

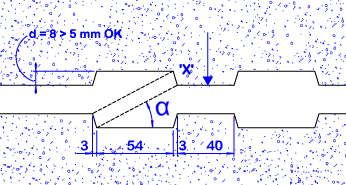
Applying IPHA Precast Concrete Structures, II edition, prof. Kim S. Elliott:
tg α = 23 / 57 α = 22º
X = 8 / cos (α) = 8,63 mm.
The root shear area is: #10 * (3+54+3) * (h=100) = 60.000 mm2
The friction at the indented zone is 0,825 N/mm2, then:
V= 0,825N/mm2 * 60.000 mm2 = 49,50 kN
On each indenting there will be: 49,50 kN / (10 teeth * cos α) = 4,95 / 0,927 = 5,33 kN
The resistance of the teeth taking the weaker concrete (poured at the joint C30/37) including the correction factor is:
fc = 5,33 kN * 1000/100*’X’ = 6,17 N/mm2
fck / ϒc = 30 / 1,5 = 20,00 N/mm2 > 6,17 N/mm2 stress on each tooth.
Since eq(1) 0,5 * ν * fcd = 0,5 * 0,6 * 20 = 6,66 N/mm2 > 6,17 N/mm2 an indenting on more than 50% of the interfacing surface would be redundant, and particular attention must be drawn on the selection of the grout pored at the shear-keyed longitudinal joints between adjacent HCS on the floors.
Note: νis strength reduction factor for concrete cracked in shear. EN1992-1-1 6.2.2.(6).

Conclusion:
In precast concrete construction, the shear key (also known as indenting or even castellated concrete surfaces) is contemplated by most of the international building codes as a mechanism for the transmission of additional shear.

Prensoland
Web : www.prensoland.com